Martingale – O que é o sistema de apostas Martingale?

Alguns apostadores acreditam piamente nas estratégias de gestão de dinheiro mas será que são tão fiáveis como as pessoas pensam? Joseph Buchdahl investigou o sistema de apostas Martingale para ver se os retornos compensam os riscos.

Existem alguns apostadores (e conselheiros) que defendem a estratégia de gestão de dinheiro, que envolve o aumento incremental do montante apostado após apostas perdidas, numa tentativa de recuperar dinheiro perdido anteriormente.

É frequentemente considerada por tais pessoas como uma estratégia segura, por entenderem que é inevitável que acabaremos por ganhar no final e, quando tal acontecer, todo o dinheiro perdido irá ser recuperado em conjunto com o lucro originalmente ambicionado da primeira aposta.

Os leitores mais astutos já terão detetado a falha: nada é inevitável no mundo das apostas. Se tal fosse assim, não seriam apostas. O motivo pelo qual alguns jogadores ignoram esta falha deve-se a alguns preconceitos heurísticos: ter excesso de confiança (de que irão ganhar) e sobrestimar a probabilidade de ocorrência de marés de azar. Este tipo de gestão de dinheiro de apostas é tradicionalmente conhecido como o sistema Martingale.

A estratégia Martingale

O plano de apostas Martingale tem origem no mundo das apostas de casino e, sobretudo, na roleta. Um jogo popular na roleta é a aposta no vermelho ou preto, no qual o apostador tem de decidir se a bola irá cair num número vermelho ou preto após cada rodada.

Ignorando a influência da vantagem da casa, as probabilidades de cada resultado são de 2,00. A ideia subjacente à estratégica básica de Martingale consiste em duplicar o montante apostado após cada aposta perdida e regressar ao montante da aposta inicial (valor de referência) após cada vitória, apesar de podermos aplicá-la a quaisquer probabilidades de apostas utilizando a expressão:

Taxa de progressão Martingale = probabilidades/probabilidades – 1)

Por exemplo, se as probabilidades de apostas forem de 3,00, a taxa de progressão do aumento do montante apostado seria de 1,5.

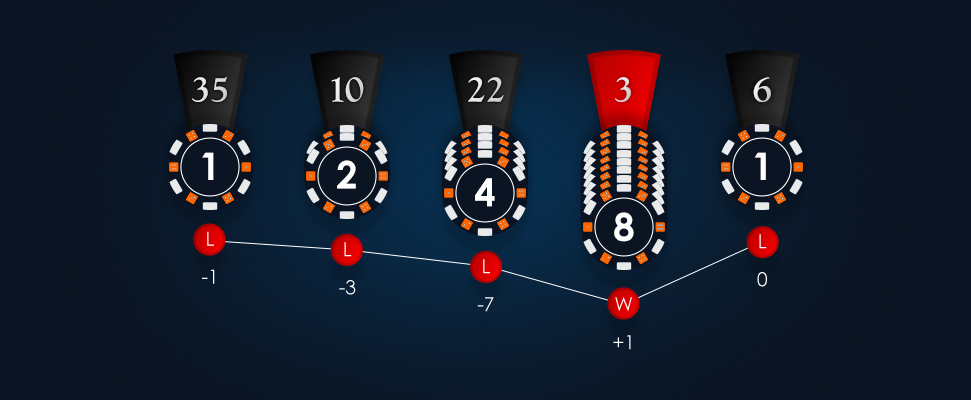
Deste modo, as perdas anteriores são recuperadas após cada resultado positivo para além do lucro originalmente ambicionado, tal como revela a seguinte sequência de rodadas.

A estratégia Martingale muda os riscos e não as expectativas matemáticas

No seu livro eletrónico, “Successful Staking Strategies” (2001), Stuart Holland deu um simples mas excelente exemplo que demonstra porque é que a estratégia Martingale é incapaz de criar algo a partir de nada.

Considere as primeiras três rodadas da roleta na sequência acima. Três cores pretas perdedoras consecutivas representam apenas 1 de 8 resultados possíveis, cada um tão provável como o outro.

A tabela em baixo apresenta a expectativa de lucro para cada uma destas 8 variação, onde V=Vermelho e P=Preto, descontando a influência da vantagem da casa (na forma do zero verde). Para calcular a expectativa para qualquer resultado, basta multiplicar o lucro ou perda efetivas para esse resultado pela probabilidade da sua ocorrência.

A soma das expectativas individuais para as 8 variações atribui a expectativa total para a estratégia. É zero. Como tal, para uma roda de roleta justa, tudo o que podemos esperar a longo prazo é atingir o ponto te equilíbrio, ou seja, não perdemos nem ganhamos.

Obviamente, as rodas de roletas verdadeiras não são justas. Um único jogo de preto/vermelho num casino comporta uma expectativa negativa e, como tal, o mesmo também acontece com a soma de muitos jogos.

Uma análise semelhante para montantes de apostas nivelados (o montante da aposta é sempre o mesmo) apresenta exatamente o mesmo resultado: uma expetativa geral de zero.

Analisemos de perto as duas tabelas. Neste exemplo, a estratégia Martingale aumentou de 4 para 5 a quantidade de vezes que podemos esperar ter lucro, relativamente a uma estratégia de montantes de aposta nivelados.

Infelizmente, tal acontece às custas de uma grande perda. Tudo o que a estratégia Martingale conquistou verdadeiramente foi uma mudança na distribuição dos riscos. Para obter um resultado extra com uma expectativa positiva assume-se uma expetativa negativa muito maior, relativamente ao resultado equivalente para montantes de aposta nivelados. Esta é a origem do perigo inerente à estratégia.

Utilizar a estratégia Martingale

Nas apostas desportivas, a estratégia Martingale poderá oferecer, aparentemente, ao apostador uma hipótese de lucrar mesmo quando o apostador não consegue garantir um valor positivo esperado, uma vez que cada vitória irá recuperar as suas perdas anteriores e adicionar um pouco extra de cada vez.

No entanto, esperemos que a análise anterior tenha convencido o leitor de que a progressão da estratégia Martingale é imperfeita matematicamente e inerentemente muito arriscada, uma vez que qualquer série prolongada de perdas consecutivas irá brevemente aumentar a dimensão do montante de aposta para níveis muito elevados. Por exemplo, dez apostas falhadas consecutivas irão exigir que a 11ª aposta seja de 1024 unidades, apenas para ganhar uma.

Consoante a dimensão do montante da aposta inicial, não se pode excluir que tal possa ultrapassar os limites aceites pela casa de apostas. Do mesmo modo, tal poderá exceder os fundos restantes na carteira do apostador.

Martingale subestimar a hipótese de ocorrência de marés de azar

Qual é a probabilidade de ter uma série de 10 perdas consecutivas com um valor monetário constante? Isoladamente, a matemática deste cálculo é fácil de fazer. Se cada aposta independente tiver uma probabilidade de perda de 50% (ou 0,5), a probabilidade de 10 perdas consecutivas será 0,510 = 0,0977%.

Uma probabilidade tão baixa engana muitas pessoas, levando-as a acreditar que a estratégia Martingale é relativamente segura de seguir. Mas qual é a probabilidade de ter uma maré de azar deste tipo, num determinado momento, durante uma série muito maior de apostas?

A matemática a fazer para este cálculo é muito mais complicada mas, de forma intuitiva, podemos reconhecer que irá ser muito mais provável do que a percentagem orçamentada para uma série individual, uma vez que existem muito mais oportunidades de que aconteça. Felizmente, existe uma forma muito útil de calcular a previsibilidade da maré de azar mais longa numa série extensa de apostas.

S_L=(Ln(N))/(Ln(O_L))

“S_L” corresponde à duração da série de azar máxima esperada, “N” corresponde ao número total de apostas efetuadas, “Ln” corresponde ao logaritmo natural (disponível em qualquer calculadora científica) e “O_L” corresponde às probabilidades de perder uma aposta individual, que podem ser calculadas a partir das probabilidades de apostas ou apostas para ganhar, “O_W”, ao:

O_L= O_W/(O_W- 1)

Por isso, por exemplo, numa série de 1000 apostas a probabilidades justas de 2,00, poderíamos esperar tipicamente pelo menos uma série de 10 perdas consecutivas. Tal como constatámos, esta série iria significar que o valor da próxima aposta teria de ser 1024 vezes superior à primeira.

Para conseguir lidar razoavelmente com a possibilidade de sofrer uma maré de azar deste género, é necessário calcular de forma apropriada a dimensão proporcional dos fundos e montante da aposta de referência do apostador. Quanto maior for a série de apostas, menor será o montante da aposta de referência como uma proporção dos fundos do apostador para lidar com os cenários mais pessimistas.

Durante uma série de 1000 apostas de valor constante, os fundos deverão ser no mínimo 1000 vezes superiores ao valor do montante da aposta de referência. Tal irá significar montantes de aposta de referência (e, consequentemente, os lucros após as perdas) tão pequenas que quase não vale a pena correr o risco de seguir a estratégia ou correr o risco de perder montantes consideravelmente grandes.

O sistema Martingale tem alto risco de bancarrota

No meu livro “Fixed Odds Sports Betting: Statistical Forecasting and Risk Management” (2003), testei a estratégia Martingale para uma série de 250 apostas no mundo real com uma expectativa média de vitória individual de 0,5 (ou seja, probabilidades de 2,00).

Para montantes de aposta de referência de 1% dos fundos iniciais, a probabilidade de terminarmos na bancarrota, assumindo que as probabilidades seriam justas, era de 53%. Para uma estratégia equivalente de montantes de aposta nivelados, a percentagem era tão pequena que correspondia efetivamente a 0%. Para um cenário onde a casa de apostas detinha uma vantagem de 5 e 10% respetivamente sobre o apostador, o risco de bancarrota para a estratégia Martingale subiu para 65% e 78%.

Mesmo para cenários onde o apostador detinha a vantagem, continuava a existir um risco considerável. Com uma vantagem de 5%, o risco era de 38%. Obviamente, quando os apostadores garantiam um valor positivo esperado através da sua capacidade de previsão, poderíamos questionar por que é que teriam sequer de correr atrás dos seus prejuízos.

O sistema Martingale é uma ilusão

Teoricamente, com fundos ilimitados, uma quantidade infinita de apostas, tempo infinito e uma casa de apostas infinitamente flexível, poderíamos argumentar que a estratégia Martingale se transforma numa estratégia vencedora.

Obviamente que poderemos questionar o motivo de alguém tentar esta estratégia, se já tem fundos ilimitados. No mundo real das apostas, a conclusão da estratégia Martingale é a seguinte: se o apostador não for bom o suficiente para vencer as probabilidades, a estratégia Martingale é o caminho mais certo para a ruína financeira. De qualquer forma, se o apostador for bom o suficiente, não precisa desta estratégia.

A aparente capacidade da estratégia Martingale de transformar perdas em lucros é, muito simplesmente, uma ilusão muito perigosa.

*Fonte: https://www.pinnacle.com/pt/betting-articles/Betting-Strategy/martingale-betting-system/G3523M233YRNPGZG